3. Participation Ratio (PR) as a Intrinsic Dimensionality Measure
In standard DBMs, the final form of the distribution \(p_T(\mathbf{x})\) approximates an isotropic Gaussian distribution, typically with unit variance. As a result, these models increase the effective dimensionality of the data, which may begin as a low-dimensional manifold embedded within \(\mathbf{R}^d\). Thus, even maintaining intrinsic data dimensionality requires both a definition of dimensionality and a choice of flow that preserves this dimension. In this work, we consider a particularly simple measure of dimensionality, the participation ratio (PR), first introduced by Gao et al., 2017:
\[PR(\boldsymbol \Sigma) = \frac{tr(\boldsymbol\Sigma)^2}{tr(\boldsymbol\Sigma^2)} = \frac{(\sum_i \sigma_i^2)^2}{\sum_i \sigma_i^4}\]where \(\boldsymbol\Sigma\) is the covariance of the data with eigenvalues \({\sigma_i^2}\). PR is invariant to linear transforms of the data, depends only on second-order statistics, is 1 when \(\boldsymbol \Sigma\) is rank-1, and is equal to the nominal dimensionality \(d\) when \(\boldsymbol \Sigma \propto \mathbf{1}_{d\times d}\).
Below we showcase zoomed in spectra (up to 25 top principal components) and the corresponding Participation-Ratio (PR) values for a couple of benchmark image datasets. Note that PR values reported are considerably smaller than ambient space data dimensionality (e.g., for CIFAR-10 ambient dimension is 3072 - 32x32x3, whereas its PR dimension is ~9). Additionally, as expected, datasets whose spectra decay faster have lower reported PR dimensonality (e.g., see SVHN vs. MNIST).
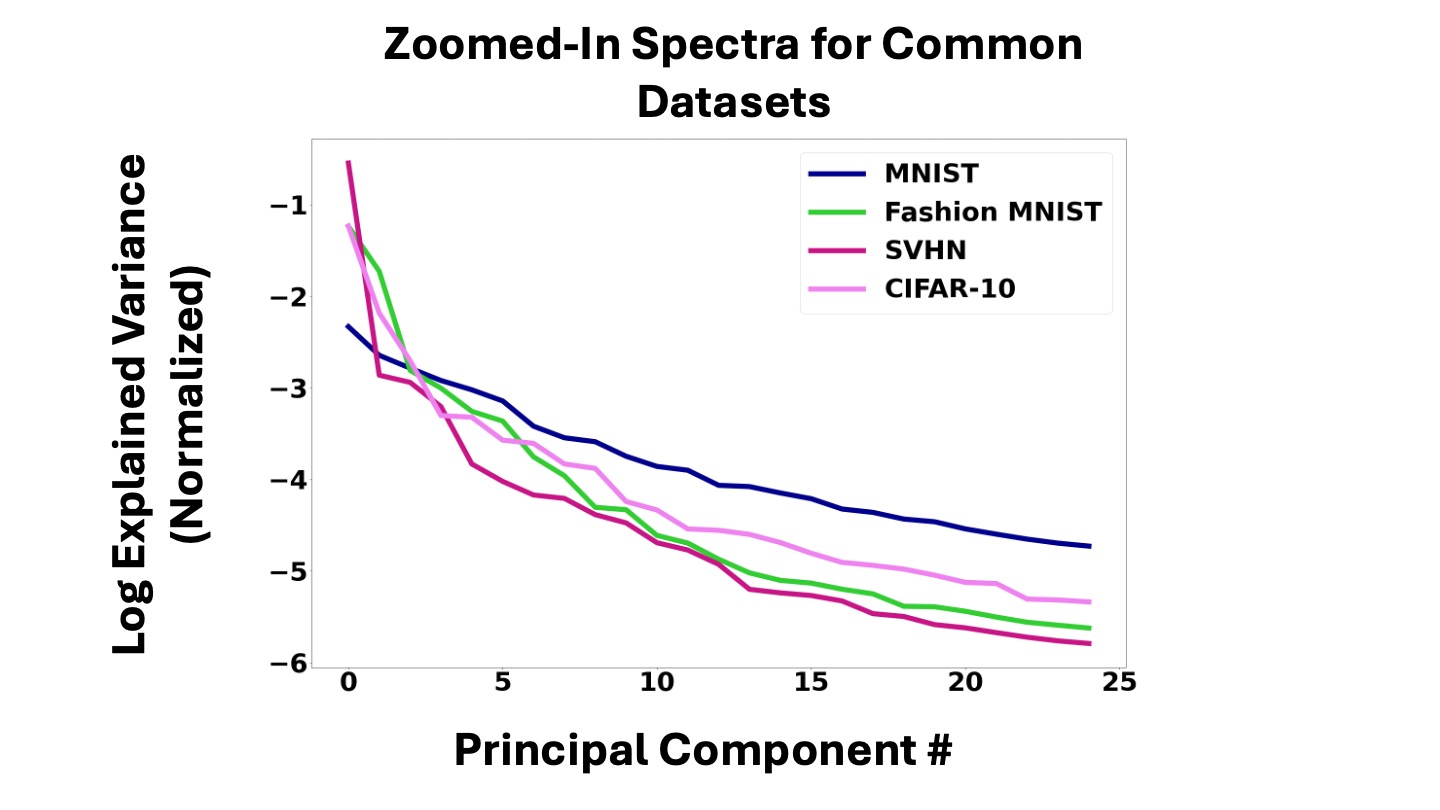
| Dataset | PR |
| MNIST | 30.69 |
| Fashion MNIST | 7.90 |
| SVHN | 2.90 |
| CIFAR-10 | 9.24 |